【Solution】Nauuo and Binary Tree-重链剖分

Posted on | In ,

题目传送门。

首先将每个点与 $1$ 号点进行一次询问，求出每个节点的深度，然后按照其深度进行分层。（方便划分子问题）

假设你已经做完了以 $1$ 为根的上面一坨，现在要求第 $i$ 个点的父亲是谁。

我们先把上面一坨拿来重链剖分，找到链底端节点，然后根据 $\texttt{LCA}$ 深度的性质跳到他们的 $\texttt{LCA}$。

如图：

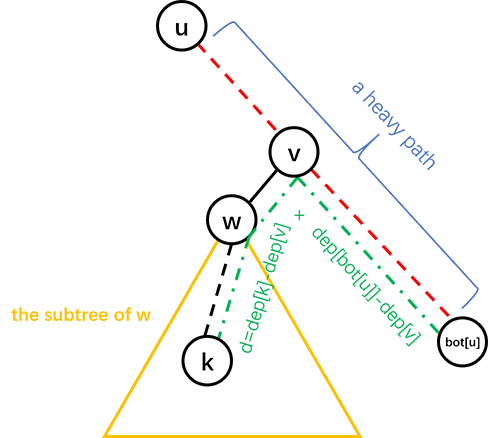
设这个点为 $v$ 。然后我们跳到他的非重儿子。设为 $w$。

那么我们相当于只要在 $w$ 为根的一坨中寻找他的父亲，这就变成了子问题。

当发现 $w$ 没有子节点的时候，你就把它挂上去，结束了。

时间复杂度分析：跳一次轻边子树大小至少 $/2$ ，因此不超过 $\log(n)$ 次就能找到父亲。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
IL void solve(int j, int r) {
  if (!p[r][0]) {
    addEdge(r, j);
    return;
  }

  int d1 = que(bot[r], j);
  int v = bot[r];

  while (dep[v] << 1 > dep[j] + dep[bot[r]] - d1)
    v = fa[v];

  int s = p[v][!son[v]];

  if (s)
    solve(j, s);
  else
    addEdge(v, j);
}

完整代码