【Algorithm Notes】Convex Hull Trick

Posted on | In ,

Intro

单调队列优化 DP 需要状态变量 $j$ 与决策变量 $k$ 分离，而遇到交叉项如 $i\times j$ 时则无能为力。因此我们需要新的方法。

Example

【例题】玩具装箱

题目传送门。

$$
\begin{align}
S_i&=\sum_{j\leq i}{C_i}+i\
f_{i, j}&=\min(f_{i - 1, k} + (S_j - S_k - L - 1)^2)\
f_{i, j}&=f_{i - 1,k} + (S_j - S_k - L-1)^2\
f_j&=f_k+S_j^2-2S_j(S_k+L+1)+(S_k+L+1)^2\
f_k+(S_k+L+1)^2&=2S_j\cdot S_k+(f_j+2(L+1)S_j-S_j^2)
\end{align}
$$

这里为了打消平方项的影响，我们直接把 $(S_k+L+1)^2$ 设置成了 $y$ 轴。

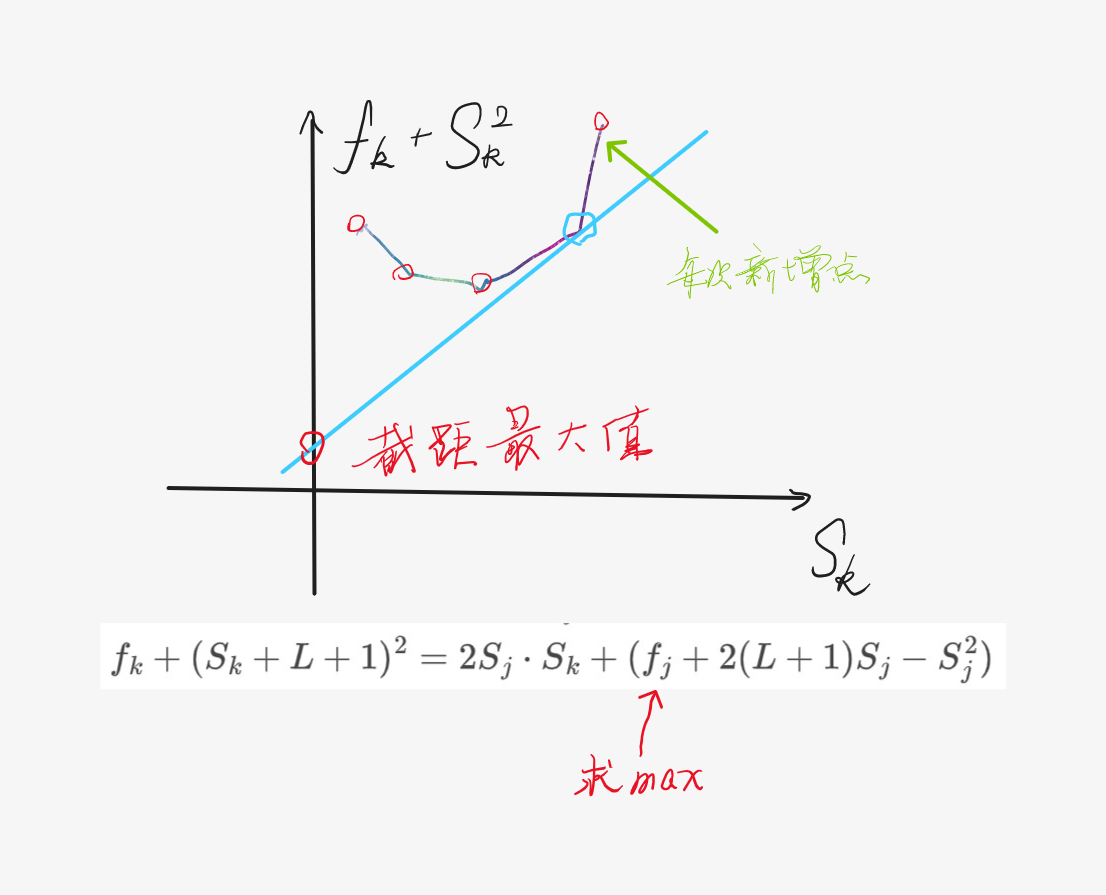
slope-1

这根直线与凸壳相交，当且仅当这个点的下方的那条凸壳上的线段的斜率 $< k$ ，而上方这条 $ \geq k$。

方法

如果 $x_i$ 从小到大依次进来：此时只需维护半个凸壳。

  1. 将所给直线与凸壳上的点从左端开始进行对比，找到斜率介于两者之间的位置取出该位置的值作为 j
  2. 按照原始方程进行转移
  3. 维护凸壳，删除多余的点，将点 $(x_i, y_i)$ 从右端加入凸壳

需要注意的是，有时候按顺序插入的点不一定在凸壳的右侧，这时候需要维护整个凸壳，并多一个 $\log$ 来二分查找点的位置。

Code

Init
1
2
3
4
5
IL void init() {
	rd<int>(n), rd<ll>(L);
	for (int i = 1; i <= n; c[i] += c[i - 1] + 1, ++i) rd<ll>(c[i]);
	for (int i = 1; i <= n; ++i) Debug("%d\n", c[i]);
}
DP
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
IL Lf slope(int u, int v) {
	Lf x_u = X(u), x_v = X(v), y_u = Y(u), y_v = Y(v);
	if (x_u == x_v) return 1e18;
	return (y_v - y_u) / (x_v - x_u);
}

IL void work() {
	int l = 1, r = 0;
	q[++r] = 0;
	for (int j = 1; j <= n; ++j) {
		while (l < r && slope(q[l], q[l + 1]) <= c[j] * 2.0)
			++l;
		f[j] = f[q[l]] + (c[j] - b(q[l])) * (c[j] - b(q[l]));
		Debug("dp[%d] is %d while using %d\n", j, f[j], l);
		while (l < r && slope(q[r - 1], q[r]) >= slope(q[r - 1], j))
			--r;
		q[++r] = j;
	}
	printf("%lld\n", f[n]);
}